The theory of Bigraphs and Bigraphical Reactive Systems (BRSs) [1] has been developed by Milner as a formalism for describing and analyzing mobile computation and pervasive systems. A BRS is a graphical model in which bigraphs can be reconfigured using reaction rules.
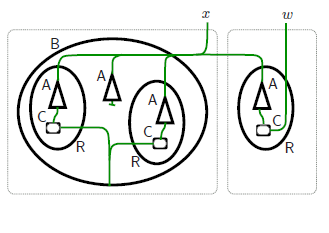
A bigraph (cf. Figure 1) consists of hyperedges and nodes that can have ports. Each hyperedge can connect many ports on different nodes. These nodes can be nested (for example, the R-node in the bigraph G is nested in the B-node). This nesting structure describes the hierarchical structure of a system entities. Whereas, a reaction rule (cf. Figure 2) consists of a redex (the pattern to be changed) and a reactum (the changed pattern). The redex and the reactum of a rule are themselves bigraphs.
 |
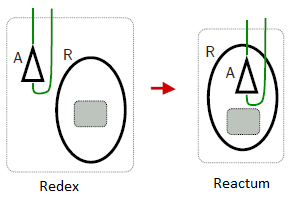 |
| Figure 1. A bigraph G [1] | Figure 2. A reaction rule [1] |
BiGMTE Presentation
BiGMTE is a tool for bigraph matching and transformation. It allows to execute the application of a reaction rule on a given bigraph to be rewritten (i.e., determines for a given bigraph B and a reaction rule R whether and how the reaction rule can be applied to rewrite the bigraph B). This execution under BiGMTE is based on graph rewirinting.
Since the theory of BRS is closely related to Graph Transformation Systems (GTSs) [4] and considering the exhaustiveness of studies on graph transformations, we provide a solution for executing BRSs relied on GTSs. As an alternative to implementing matching for bigraphs, we tried to formalize BRSs as GTSs and applied then graph matching algorithms on bigraphs. By this way, we can benefit from existing tools and techniques developed for graph transformations. We initiated an investigation of how to simulate a BRS with a GTS. Our solution follows three steps. The first step consists in encoding a bigraph into a graph. The second step consists in simulating the application of a reaction rule with a graph rule. And finally the third step allows the encoding of the resulted graphs into a bigraphs.
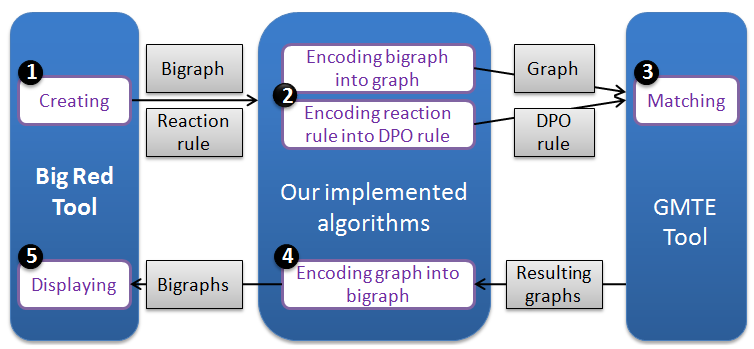
BiGMTE Architecture BiGMTE is an integration of some existing tools. It uses Big Red [2], a graphical editor allowing to create and edit bigraphs and reaction rules. Besides, it is based on GMTE [3], a tool for graph matching and transformation. Therofore, the matching and the transformation procedure performs five steps as highlighted in Figure 3:
- BRS creating: Using Big Red the user creates a BRS (Bigraphs and reaction rules). The edited BRS is exported into an XML file.
- BRS translating: This XML file is parsed to be the input of our implemented algorithms. The first algorithm translates the edited bigraph to a graph and the second one translates the edited reaction rule to a graph rule.
- Graph matching: The obtained graph rule is executed and applied on the obtained graph using GMTE.
- Graph translating: After the rule application, the resulting graphs generated by GMTE are translated in turn to bigraphs.
- Displaying: The obtained bigraphs are displayed by Big Red.
References
| [1] |
Robin Milner. The Space and Motion of Communicating Agents. Cambridge University Press, 2009. |
| [2] |
Alexander John Faithfull, Gian Perrone, and Thomas T. Hildebrandt. Big red: A development environment for bigraphs. ECEASST, 61, 2013. |
| [3] |
MohamedAmine Hannachi, Ismael Bouassida Rodriguez, Khalil Drira, and SaulEduardo Pomares Hernandez. Gmte: A tool for graph transformation and exact/inexact graph matching. In Graph-Based Representations in Pattern Recognition, pages 71-80, 2013. |
| [4] |
Ehrig, H., Pfender, M., Schneider, H.: Graph-grammars: An algebraic approach. In: Switching and Automata Theory, 1973. IEEE Conference Record of 14th Annual Symposium on, pages 167-180, 1973. |